




| 𝕲𝖊𝖔𝖒𝖊𝖙𝖗𝖎𝖈 𝕬𝖗𝖒𝖆𝖙𝖚𝖗𝖊𝖘 | ||
|---|---|---|
| A while ago, before the plague was really upon us, I had went on a hike with a colleague of mine (who by my reckoning, would prefer to remain unnamed, though anyone who really, truly has gotten to know me, whether as a friend or as a stalker, could probably guess who this friend is) during the bleak and cold January. The scene was abysmally gray, but the park was totally devoid of all people, which was the only factor to my liking. My colleague, who I shall denote as SZLK from hereafter, has a strong interest in buried treasures around the world, and the mysteries surrounding them. On our many drive-abouts and hikes, he always brings up new developments or interesting facts about treasures that he's learned about, though usually it's the same treasures. One in particular, is allegedly on Oak Island, possibly located within this triangular, man-made swamp. On this January hike, SZLK brings the treasure to my attention once again, but this time adds in a fact that he hasn't theretofore mentioned; the association of an artist to the mystery. Nicolas Poussin, a French born artist, had made paintings that allegedly are secret maps. I have seen some examples of these maps, and want to believe that the conspiracy theory is true. So I do. SZLK and I talk a little more about Poussin, I ask some basic questions regarding relation of the artist to the Oak Island treasure, and then we go to his house for warm drink. While there, we pull up a search for a documentary, any documentary, regarding Poussin, and find a lecture about his painting, Et In Arcadia Ego, which is titled Guy Patton: Poussin’s Arcadian Vision: Search for the Golden Age. We watched this talk in anticipation that he might talk about the treasure, but we found that he was more interested in other properties concerning the painting itself. One particular point of interest he had brought up was the secret geometrical properties of the painting, which was a lot more fascinating to me than it was to SZLK. I came away from that talk with a newfound appreciation for the more technical approach to art than I originally had. For a while, I only cared about painting freely with no guides, because I thought it was too difficult and restrictive. But now I have come to appreciate the use of secret geometry to structure a painting. Very recently, I have used what's called the armature of the rectangle to order a painting I made featuring a garden and a somber individual resting there. Prior to this, I had only really known about the rule of thirds. But now I realize that the rule of thirds can just as well be fitted to this armature, which provides for more robust and powerful guides. |
 |
|
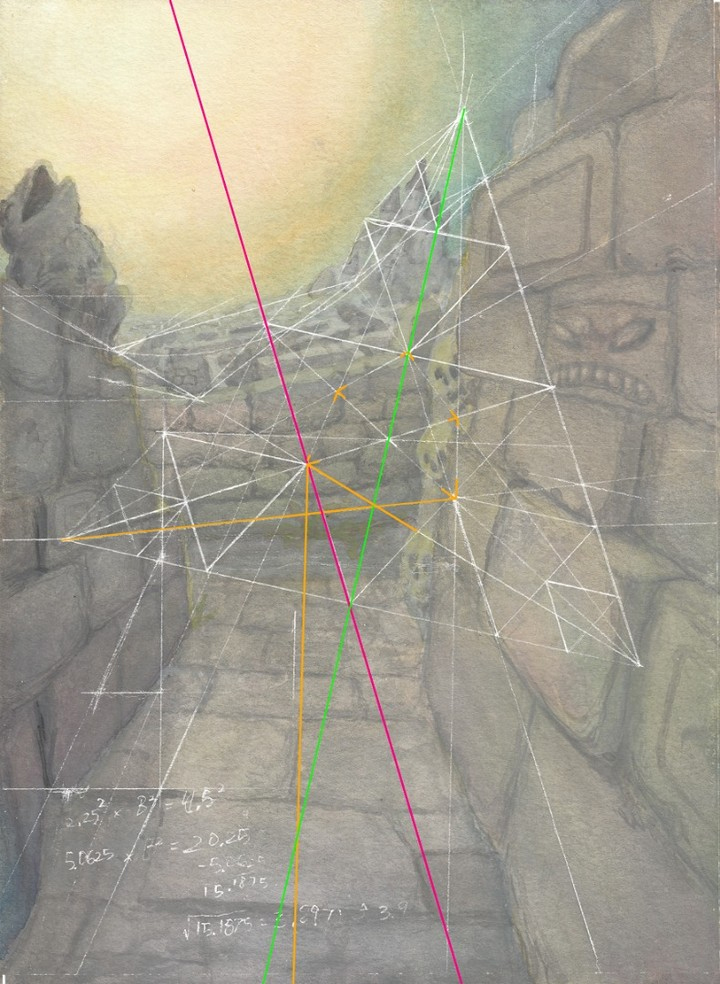 |
Just yesterday, I had spent the whole day discovering angles using the Sierpiński Triangle, an ancient fractal proven by a man of Polish birth. This is a fractal that comprises of an equilateral triangle, with another equilateral triangle, 1/2 its size, and inverted, removed from the center. All three corners of the smaller triangle make contact with the center of the sides of the original triangle. Splitting both triangles in half, starting from and ending at all 3 of their respective corners, you can find the exact point which you must intersect to split the triangle equally into three from each corner. The point is at the center of the sides of the inner triangle. Drawing a line from each corner, through each point, to the opposite side of the triangle, will give you 9 angles of 20°. This is especially useful for making nine sided shapes. The beauty of this method, too, is that it can be achieved with nothing more than a ruler and a pen. You can use the ruler to first make a square grid, then, using Pythagorean theorem, you can solve for the height of the triangle, using half of the width, and the full width for A² and C² respectively. For example; To solve for H of an equilateral triangle of 7 inches.. A² + B² = C² 3.5² + B² = 7² 12.25 + B² = 49 49 - 12.25 = 36.75 √36.75 = 6.062 = B H = 6.062 inches |
|
| Starting from the center of your baseline for the triangle (which in this example is 7", therefore the center is at 3.5 inches), and placing your ruler exactly perpendicular (or as close to) to that line, you can measure from there, up to 6.062 inches, and place a point there, which you can connect to the ends of the baseline, and the newly made lines should be the same length (in this case, 7"). From there, you can make the fractal as previously described, and find angles by bisecting certain angles and points. I mention this triangle and the angles therein because, using this as a new armature, an armature of the Sierpiński triangle, interests me greatly. I may end up using it, or some variation of it, to achieve what I hope to be an incredible artistic endeavor, though not one of high achievement, probably not even of any novelty, but it will suffice to add another layer of depth to my work, I think, which will delight those who possess the cleverness, and possibly this inside knowledge, required to see it's fruition. Using these guides as a sort of anchor point, I hope that one day, one might be able to layer my future paintings to create a whole new image. And, with my love of secrets in mind, I may try to use this theory to create some secret image of my own. Perhaps I'll make a map like Poussin did in a couple of his paintings. I mentioned before that if I'm going to be pursuing art long term, I better go as deep as I possibly can so that it may live up to my desires for what it can be; a truly profound and interactive/immersive cerebral experience. |
||